本記事は、TensorFlow(テンソルフロー)の本家サイト「MNIST For ML Beginners」 を翻訳(適宜意訳)したものです。
誤り等あればご指摘いただけたら幸いです。
はじめに
このチュートリアルは、機械学習とTensorFlowを初めて利用する読者を対象としています。あなたはすでにMNISTが何であるか、そしてSoftmax Regression1が何であるか知っていれば、このペースの速いチュートリアルを気にいるかもしれません。いずれかのチュートリアルを開始する前に、まずはTensorFlowをインストールしてください。
プログラミング方法を学ぶ際に、最初にやることは「Hello World」を出力してみる、という習わしがあります。プログラミングにHello Worldがあるように、機械学習にはMNISTがあります。
MNISTは、単純なコンピュータビジョンのデータセットです。次のような手書き数字の画像で構成されています。
また、各画像にはラベル情報が含まれていて、それがどの桁であるかを示しています。たとえば、上記の画像のラベルは「5」「0」「4」「1」になります。
このチュートリアルでは、画像を見て、その数字が何かを予測するモデルを作り、そのモデルをトレーニングします。このチュートリアルでの目標は、最先端のパフォーマンスを実現する精巧なモデルをトレーニングすることではありません。本記事の後半でコードを記載しますが、TensorFlowを使うことに足を踏み入れることです。Softmax Regression2と呼ばれる非常にシンプルなモデルから始めます。
このチュートリアルの実際のコードは非常に短く、3行程度のものしかありません。しかし、その背後にある考え方、TensorFlowがどのように動作するか、そして機械学習の考え方(概念)の両方を理解することが非常に大切です。そういった点に注目して慎重にコードを実行していきましょう。
このチュートリアルについて
このチュートリアルでは、mnist_softmax.pyコードで何が起こっているかを一行ずつ説明していきます。
このチュートリアルは、次のようないくつかの方法で利用できます。
- 各説明を読んで、各コードスニペットをコピーしてPython環境に貼り付けてください
- 解説の前後で
mnist_softmax.pyプログラムを実行し、理解が不明なコード行で何が行われているか理解してください
このチュートリアルの目標
- MNISTデータとSoftmax Regressionについて学ぶ
- イメージ内のすべてのピクセルを見ることに基づいて、数字を認識するためのモデルである関数を作成する
- TensorFlowを使用して、数千のサンプルデータを使い、数字を認識させるようにモデルをトレーニングする
- テストデータでモデルの精度を確認する
MNISTデータ
MNISTデータはYann LeCunのウェブサイトでホストされています。このチュートリアルのコードをコピーして貼り付ける場合は、データを自動的にダウンロードして読み込む次の2行のコードを記載してください。
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
MNISTデータは、トレーニングデータ(mnist.train)の55,000データポイント、テストデータ(mnist.test)の10,000ポイント、および検証データ(mnist.validation)の5,000ポイントの3種類に分割されます。
この分割は非常に重要です。機械学習では、学習に使われていないテスト用データが必要です。トレーニングデータを使って学習した後に、モデルが一般化されていることをテストデータを使って確認することが必要です。
先に述べたように、各MNISTデータポイントは、2つの部分、手書き数字の画像と対応するラベルを持ちます。
イメージを「x」、ラベルを「y」とします。トレーニングデータセットとテストデータセットの両方に画像と対応するラベルが含まれています。例えば、トレーニング画像はmnist.train.imagesで、トレーニングラベルはmnist.train.labelsとなります。
各画像は、28ピクセル×28ピクセルです。これを以下イメージのように、数値の配列として解釈します
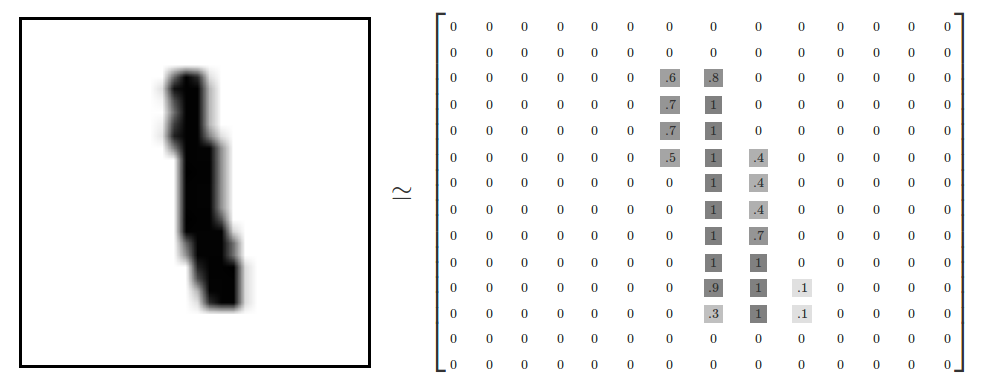
この配列を、28x28 = 784の数のベクトルに平坦化することができます。画像間で一貫している限り、配列をどのように平坦化するかは大きな問題はありません。この観点から、MNIST画像は、非常にリッチな構造を備えた、784次元のベクトル空間における単なるポイントの集まりとして見ることができます。
データを平坦化すると、画像の2D構造に関する情報が捨てられてしまします。これはまずくないでしょうか? ベストなコンピュータ・ビジョンの方法ではこの構造を利用しますので、後のチュートリアルで説明します。しかし、ここで使用する単純な方法「Softmax Regression」では利用しません。
結果は、mnist.train.imagesは[55000、784]という形のテンソル(n次元配列)になります。1番目の次元は画像のリストへのインデックスで、2番目の次元は各画像の各ピクセルのインデックスになります。テンソルの各要素は、特定の画像の特定のピクセルのための 0 と 1 の間のピクセル濃度になります。

MNISTの各画像には、対応するラベルが付いています。ラベルは0から9の間の数字で表されます。
このチュートリアルでは、ラベルを「one-hot(ワン・ホット)ベクトル」にしたいと考えています。one-hotベクトルは、ほとんどの次元で0であり、単一次元で1であるベクトルです。この場合、n番目の桁は、n番目の次元で1であるベクトルとして表されます。たとえば、3は[0,0,0,1,0,0,0,0,0,0]になります。したがって、mnist.train.labelsは[55000、10]のfloat配列になります。
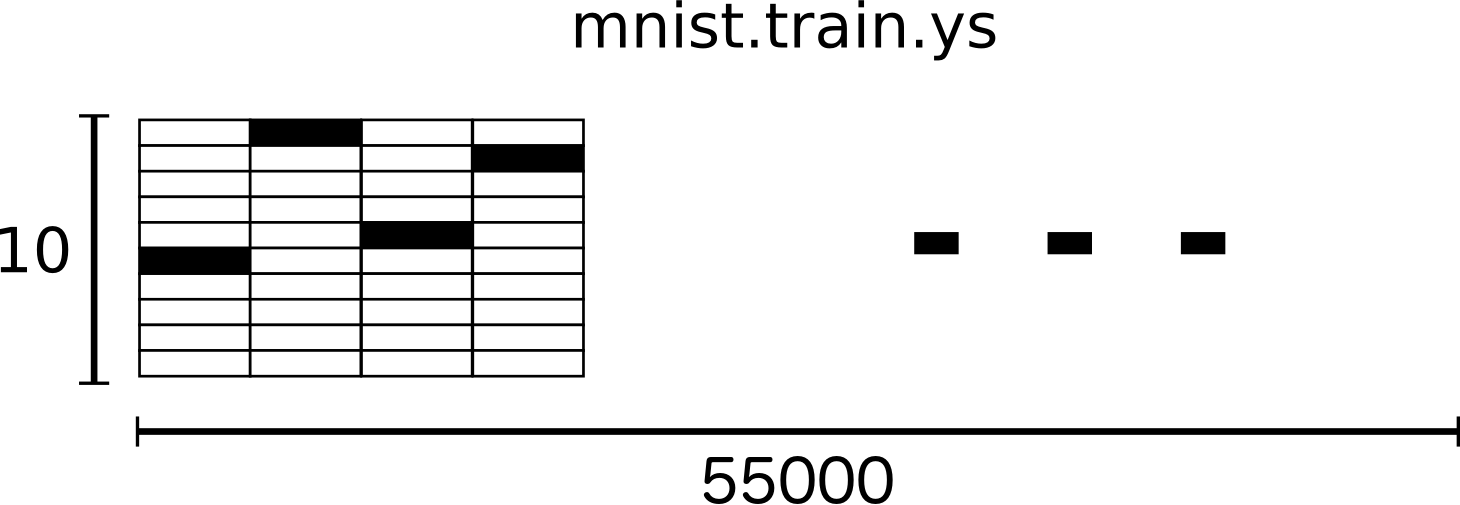
これで実際にモデルを作る準備が整いました!
Softmax Regression (多クラスロジスティック回帰)
私たちは、MNISTのすべての画像が、0と9の間の手書き数字であることを知っています。なので、与えられたイメージが可能性のあるものは10種類しかありません。私たちは、画像を見て、それが各々の数字である確率を与えたいわけです。例えば、私たちのモデルは9の画像を見て、それが9であることを80%確信しているかもしれませんが、その画像が8である確率は5%あります。その画像が、9であることは、100%確実ではないわけです。
これは、Softmax Regressionが自然でシンプルなモデルである典型的なケースです。いくつかの異なるものの1つであるオブジェクトに確率を割り当てる場合、softmaxが(合計すると1になる)0と1の間の値のリストを与えてくれます。後に、より洗練されたモデルを訓練する際にも、最後のステップはsoftmaxのレイヤーになります。
Softmax Regressionには2つのステップがあります。まず1つは、入力の確実と考えるクラスに属するための証拠 (エビデンス) を集計すること、そして証拠を確率に変換します。
与えられた画像が特定のクラスにあるという証拠を集計するために、ピクセル強度の加重和を行います(重みつき和)。その強度が高いピクセルがそのクラスにある画像に対する証拠である場合には重みが負(ネガティブ)であり、証拠が好ましい場合には肯定的(ポジティブ)ということになります。
次の図は、これらのクラスのそれぞれについて学習した1つのモデルの重みを表現しています。赤は負(ネガティブ)の重みを表し、青は正(ポジティブ)の重みを表します。
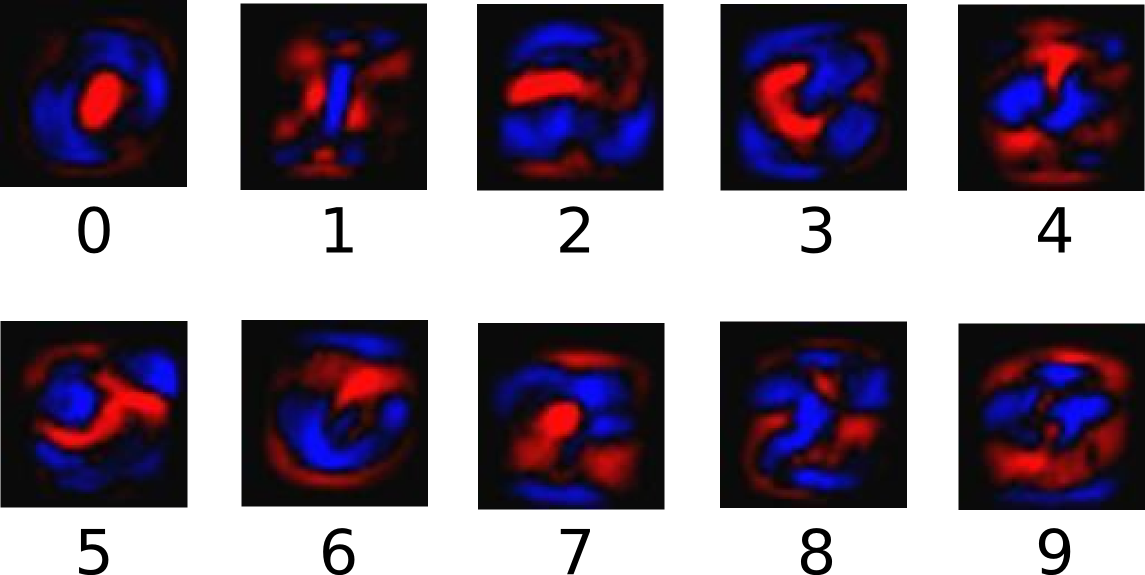
さらに、バイアス3と呼ばれる特別な証拠を追加します。基本的には、入力から独立したある事象の可能性があると言うことができるからです。その結果、入力xを与えられたクラスiの証拠は次のようになります。
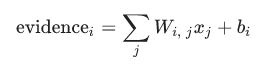
ここで、Wiは重みであり、biはクラスiのバイアスです。そして、jは入力画像xのピクセルを集計するためのインデックスです。 次に、「softmax」関数を使用して、証拠の合計を予測確率yに変換します。
![]()
ここでsoftmaxは、「活性化」または「リンク」関数として機能し、私たちの線形関数の出力を必要な形、この場合は10以上の確率分布に整形します。これは、各クラスの入力である可能性の高い証拠に変換するものとして考えることができます。次のように定義されます。
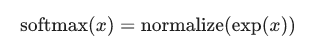
この式を展開すると、次のようになります。
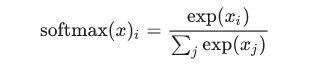
しかし、softmaxを最初の方法4で考えることは、しばしば役に立ちます。べき乗は、証拠の1単位が、仮説に与えられた重みを乗法的に増加することを意味します。逆に、証拠の1単位が少なくなることは、仮説に以前の重みのわずかな減少を与えられることを意味します。どんな仮説も、0や負の重みを持つことはありません。Softmaxはこれらの重みを正規化し、結果、総計が1になり、有効な確率分布を形成します。 (softmax関数についてより直感的な知識を得るには、Michael Nielsenの本の中のSoftmaxセクションを参照してください。)
Softmax Regressionを次の図ように表現することができます。実際にはより多くのxがあります。各出力に対して、xの重みの合計を計算し、バイアスを加えて、softmaxを適用します。
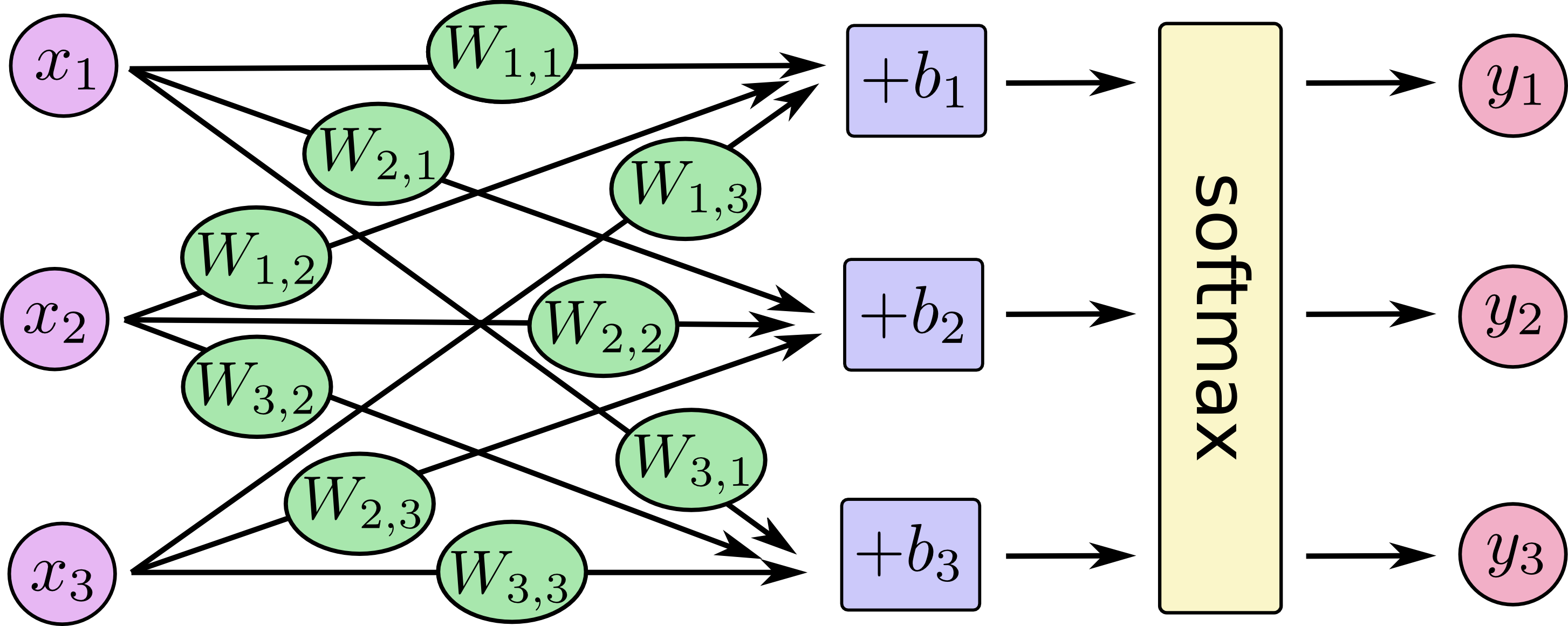
これを数式で書くと、次のようになります。
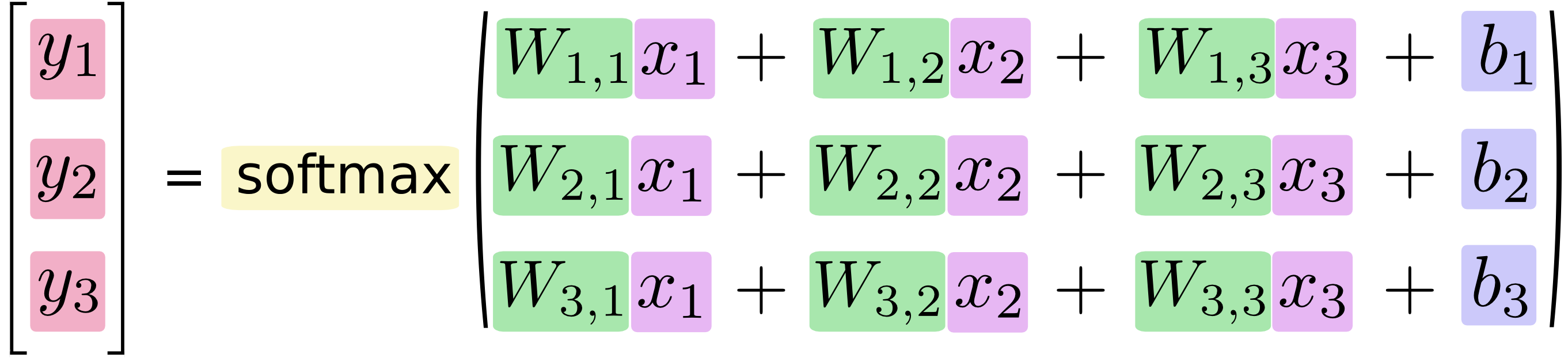
このプロシージャを「ベクトル化」して行列の乗算とベクトル加算に変換することができます。 これは計算効率のために役立ちます。
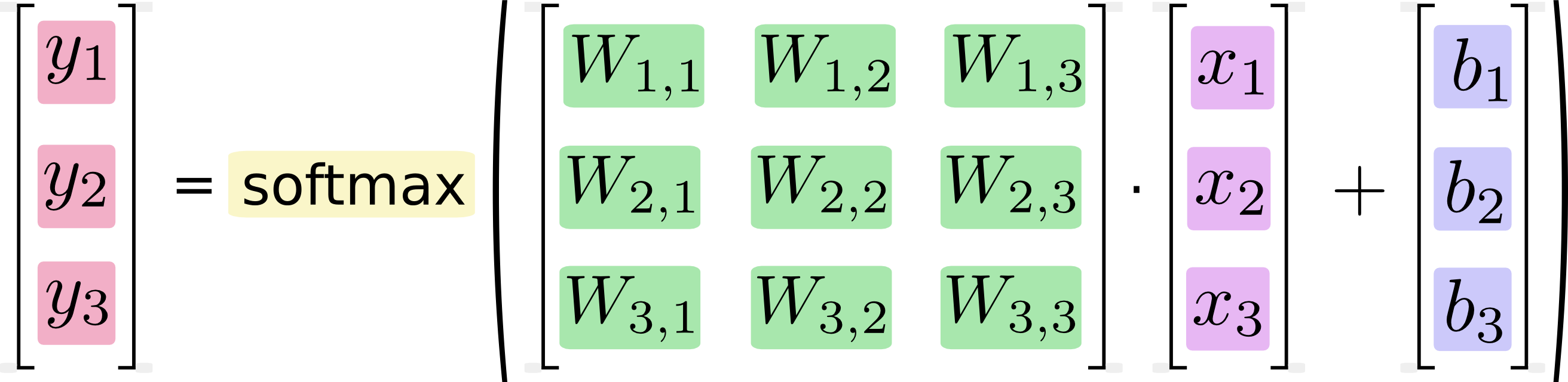
よりコンパクトに、次のように書くことができます:
![]()
それでは、上記の内容を、TensorFlowで利用できるものにしてみましょう。
回帰を実装する
Pythonで効率的な数値計算を行うためには、通常、NumPyのようなライブラリを使用します。しかし残念ながら、すべての操作をPythonに切り替えることにはまだ多くのオーバーヘッドがあります。このオーバーヘッドは、GPUで計算を実行する場合や、データを転送するコストが高い場合など、分散した方法で計算を実行する場合に特に悪いことです。
TensorFlowはPythonでも重い演算をしていますが、このオーバーヘッドを避けるためにさらに一歩前進しています。TensorFlowは、Pythonから独立した高価な操作を単独で実行する代わりに、Pythonの外で実行される演算のグラフを記述することができます。(このようなアプローチは、いくつかの機械学習ライブラリで見ることができます。)
TensorFlowを使用するには、まずインポートする必要があります。
import tensorflow as tf
シンボリック変数を操作することによって、これらの相互作用について説明します。 1つ作成してみましょう。
x = tf.placeholder(tf.float32, [None, 784])
上記のxは、特定の値ではありません。 これはプレースホルダで、TensorFlowに計算を実行するように依頼するときに入力する値です。 私たちは、784次元ベクトルに平坦化された任意の数のMNIST画像を入力できるようにしたいと考えています。これを浮動小数点数の2次元テンソルとして表現します。形状は[None、784]です。 (ここでは、Noneは次元が任意の長さであることを意味します)。
私たちのモデルには重みとバイアスも必要です。これらを追加の入力のように扱うことも考えられますが、TensorFlowはそれを処理するさらに優れた方法を持っています。変数5です。変数は変更可能なテンソルで、相互作用の演算の TensorFlow のグラフの中で有効です。計算によって利用され、変更も可能です。機械学習アプリケーションでは、一般にモデルパラメータとして、変数sを持ちます。
W = tf.Variable(tf.zeros([784, 10])) b = tf.Variable(tf.zeros([10]))
tf.Variableに変数の初期値を与えることによってこれらの変数を作成します。この場合、Wとbの両方を全て0のテンソルとして初期化します。WとBを学ぶつもりなので、最初はどんな値でも問題はありません。
Wが[784、10]の形をしていることに注目してください。なぜなら、784次元の画像ベクトルに乗算することで、差分クラスの証拠の10次元ベクトルを生成することになるからです。bは[10]の形をしていて、出力に加算することができます。
ここでモデルを実装できます。上記を定義するためには、1行だけ記述すれば良いだけです!
y = tf.nn.softmax(tf.matmul(x, W) + b)
まず、xをWにtf.matmul(x、W)という式で乗算します。これは、先ほどの数式でそれらを乗算した時とは順序が反転していますが、これはxを複数の入力をもつ2Dテンソルとして扱うための小さなトリックです次に、bを加算し、最後にtf.nn.softmaxを適用しています。
これでおしまいです。数行のセットアップの記述の後に、私たちのモデルを定義するのに1行しか必要ありません。これは、TensorFlowがSoftmax Regressionを特に簡単にするために設計されているからではありません。Tensorflowが、機械学習モデルから物理シミュレーションまで、さまざまな数値計算を記述するための非常に柔軟だからです。一度定義したモデルは、コンピュータのCPU、GPU、さらには携帯電話など、さまざまなデバイスで実行することができます!
トレーニングする
私たちのモデルを訓練するためには、「モデルが良い」とは何を意味するのか、ということを定義する必要があります。 実際には、機械学習では、一般に、「モデルが悪い」ことは何を意味するかを定義します。これをコストまたは損失(loss)と呼び、モデルが期待した結果からどれだけ離れているかを表します。その誤差を最小限に抑えようとし、エラーとの差が小さければ小さいほどモデルは良くなります。
モデルの損失を決定する一般的で非常に優れた関数に「クロスエントロピー6」というものがあります。クロスエントロピーは、情報理論の情報を圧縮する情報を考えることから発生しています。ギャンブルから機械学習まで、多くの分野で重要なアイデアとなっています。クロスエントロピーは次のように定義されます。
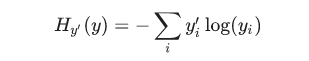
ここでのyは予測確率分布、y′は真の分布7です。大雑把な意味では、クロスエントロピーは、我々の予測がどれだけ非効率的であるかを測定しています。クロスエントロピーの詳細については、このチュートリアルの範囲を超えますが、理解を深めるだけの価値は十分にあります。
クロスエントロピーを実装するには、最初に正しい答えを入力するための新しいプレースホルダを追加する必要があります。
y_ = tf.placeholder(tf.float32, [None, 10])
次に、クロスエントロピー関数を実装することができます。以下が式です。
![]()
上記の式の記述は以下になります。
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1]))
まず、tf.logはyの各要素の対数を計算します。次に、y_の各要素にtf.log(y)の該当する要素を乗算します。次に、reduction_indices = [1]パラメータによって、tf.reduce_sumはyの2番目の次元に要素を加算します。最後に、tf.reduce_meanがバッチ内のすべてのサンプルの平均を計算します。
ソースコードでは、数値的に不安定であるため、この式を使っていないことに注意してください。代わりに、正規化されていないlogits上で tf.nn.softmax_cross_entropy_with_logitsを適用しています (e.g., tf.matmul(x, W) + b 上で softmax_cross_entropy_with_logits を呼び出す)。なぜかというと、数値的により安定的な関数が内部的に softmax 活性を計算するからです。実際のあなたのコードでは、代わりにtf.nn.softmax_cross_entropy_with_logitsを使用することを検討してください。
私たちのモデルが何をしたいかがわかったので、TensorFlowにそれをトレーニングさせるのはとても簡単です。TensorFlowは計算のグラフ全体を把握しているため、自動的にバックプロパゲーションアルゴリズムを使用して、変数がどのように(最小化したい)コストに影響を与えるか効率的に判断できます。そして、最適化アルゴリズムの選択を適用して変数を変更し、コストを減らしていくことができます。
train_step = tf.train.GradientDescentOptimizer(0.05).minimize(cross_entropy)
この場合、TensorFlowに、学習率0.5の勾配降下アルゴリズムを使用してcross_entropyを最小にするようにします。勾配降下は簡単な手順です。TensorFlowは、コストを削減する方向に各変数を少しシフトさせていきます。しかし、TensorFlowは他の多くの最適化アルゴリズムも提供しています。プログラムを1行だけ微調整するだけで簡単に使用できます。
ここでTensorFlowが裏で実際に行うことは、バックプロパゲーションと勾配降下法を実装する新しい演算をグラフに追加することです。そして、実行時に勾配降下訓練のステップを行い、変数を微調整して損失を減らすひとつの演算を返します。
これで、InteractiveSessionでモデルを起動できます。
sess = tf.InteractiveSession()
まず最初に、作成した変数を初期化する操作を作成します。
tf.global_variables_initializer().run()
トレーニングしましょう – 1000回のトレーニングステップを実行します!
for _ in range(1000):
batch_xs, batch_ys = mnist.train.next_batch(100)
sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})
ループの各ステップでは、トレーニングセットから100個のランダムなデータポイントの「バッチ」を取得します。バッチデータをtrain_stepフィードで実行して、プレースホルダを置き換えます。
ランダムなデータの小さなバッチを使用することを「stochastic training8」 – この場合は、確率的勾配降下と呼ばれます。理想的には、訓練のすべての段階ですべてのデータを使用したいです。なぜなら、全てのデータを使うことで、モデルは何をすべきかをよりよく理解できるからです。しかし、それは高くつきます。そこで代わりに、毎回異なるサブセットを使用するわけです。これは安価であり、かつ同様な多くの恩恵があります。
モデルを評価する
私たちのモデルはどれくらいうまくいくでしょうか?
それでは、まず最初に正しいラベルを予測した場所を見つてみましょう。tf.argmaxは、ある軸に沿ったテンソルの最も高い要素のインデックスを与える非常に便利な関数です。たとえば、tf.argmax(y、1)はモデルが予測する一番ありそうなラベルで、tf.argmax(y_、1)は正解のラベルです。 予測が正解と合っているか確認するためにはtf.equalが利用できます。
correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))
これはBooleanのリストを返します。どのくらいの割合で正しいかを判断するために、浮動小数点数にキャストしてから平均を取ります。たとえば、[True、False、True、True]は[1,0,1,1]になり、0.75ということになります。
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
最後に、テストデータの精度を求めます。
print(sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))
約92%になるはずです。
この結果は良い精度でしょうか? 実は、それほどよくないです。もっと言うと、かなり悪い精度です。なぜかというと、このモデルは非常に単純なモデルを使用しているからです。もう少し変更を加えれば、精度は97%にすることができます。ベストなモデルは 99.7% を超えた精度に到達可能です!(詳細については、この結果リストをご覧ください)。
重要なことは、ここで出た精度ではなく、ここで作ったモデルから学んだ内容です。もしそれでも、ここでの結果について気になっているのであれば、次のチュートリアル[English]をよく調べて、TensorFlowを使ってより洗練されたモデルを構築する方法を学んでください!



